Leçon : Équilibre d’un corps rigide sous l’action de couples coplanaires Mathématiques

Commencer à s’entraîner

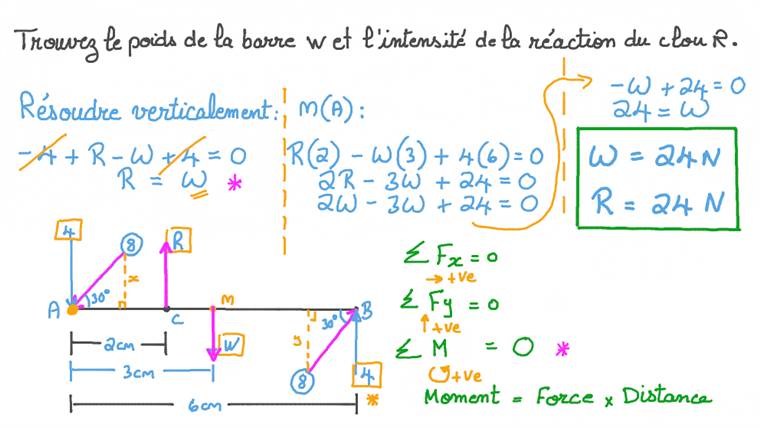
Dans cette leçon, nous allons apprendre comment étudier l'équilibre d'un corps rigide sous l'action de deux ou plusieurs couples coplanaires.

Plan de la leçon

Les élèves pourront

comprendre la relation entre deux ou plusieurs couples et l’équilibre d’un corps,
déterminer si un corps est en équilibre sous l’action de deux ou plusieurs couples,
utiliser des faits sur les couples et l’équilibre pour résoudre des problèmes.