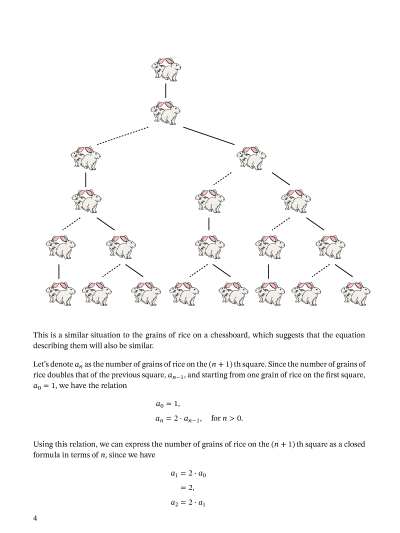
Lesson: Exponential Growth and Decay Mathematics

Start Practising

In this lesson, we will learn how to set up and solve exponential growth and decay equations and how to interpret their solutions.

Lesson Plan

Students will be able to

determine when an exponential equation represents growth or decay, namely, whether the base of the exponential function is between 0 and 1 or greater than 1,
make deductions about growth and decay based on an equation, for example, determining growth or decay rates or initial population,
graph exponential growth and decay problems,
solve exponential growth and decay problems given an equation, for example, calculating a population after a given number of years/hours,
derive the growth or decay equation from a question to find the solution to the problem,
interpret the solutions to growth and decay problems.