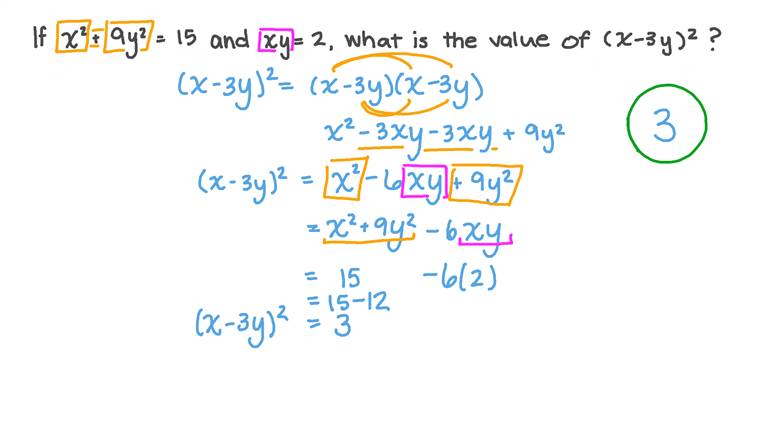Lesson: Multiplying Binomials Mathematics

In this lesson, we will learn how to multiply two binomials using different methods such as FOIL or the vertical method.

Lesson Plan

Students will be able to

multiply two different binomials,
use the FOIL method and grid method to facilitate the multiplication of two binomials,
multiply a binomial by itself (i.e., square a binomial),
multiply two binomials where the result is a difference of squares,
find unknowns in algebraic expressions by multiplying binomials,
solve geometric problems using the multiplication of binomials.

Q1:

Expand and simplify .

Q2:

Expand the product .

Q3:

Expand the product .