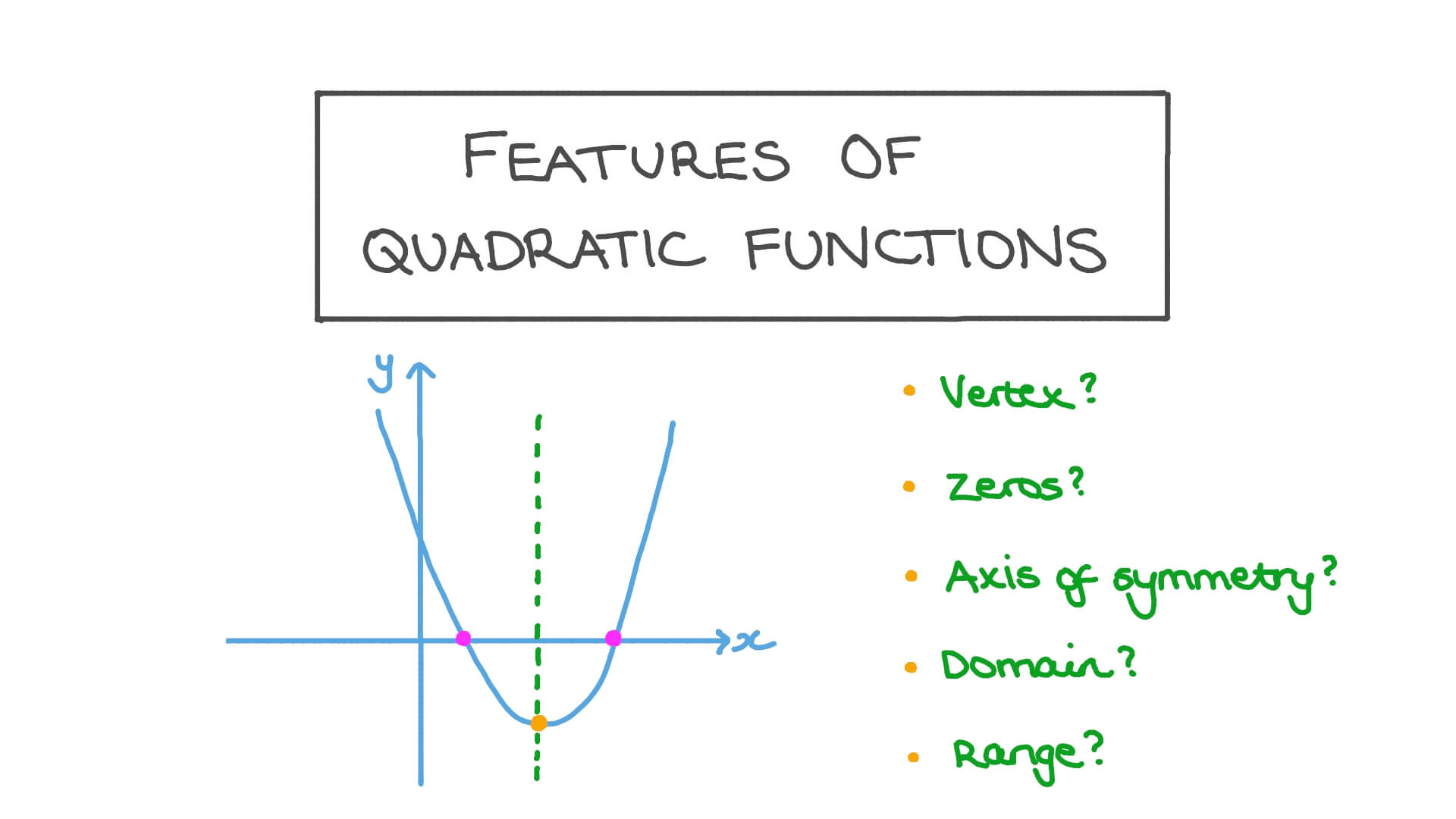
Lesson: Features of Quadratic Functions Mathematics

In this lesson, we will learn how to identify features of quadratic functions, such as its vertex, extrema, axis of symmetry, domain, and range.

Lesson Video

Lesson Playlist

02:06
05:20
+1

02:26

Lesson Worksheet

Q1:

Find the coordinates of the vertex of the function .

Q2:

Find the coordinates of the vertex of the graph of . State the value of the function at the vertex and determine whether it is a maximum or minimum value.

Q3:

Find the axis of symmetry of the graph of .