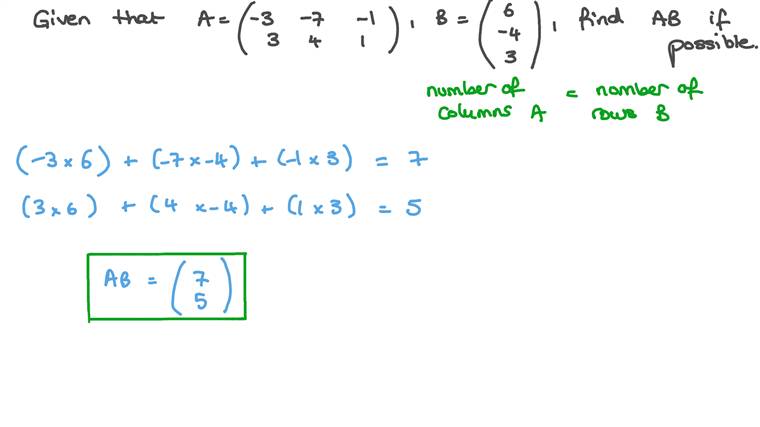Lesson: Matrix Multiplication Mathematics

In this lesson, we will learn how to identify the conditions for matrix multiplication and evaluate the product of two matrices if possible.

Lesson Plan

Students will be able to

Q1:

Fill in the blank: If matrix is of order and matrix is of order , then matrix is of order .

Q2:

Given that is a matrix of order , and is a matrix of order , determine the condition under which is defined.

Q3:

Consider the matrices Find , if possible.