Lesson: Partitioning a Line Segment on the Coordinate Plane Mathematics
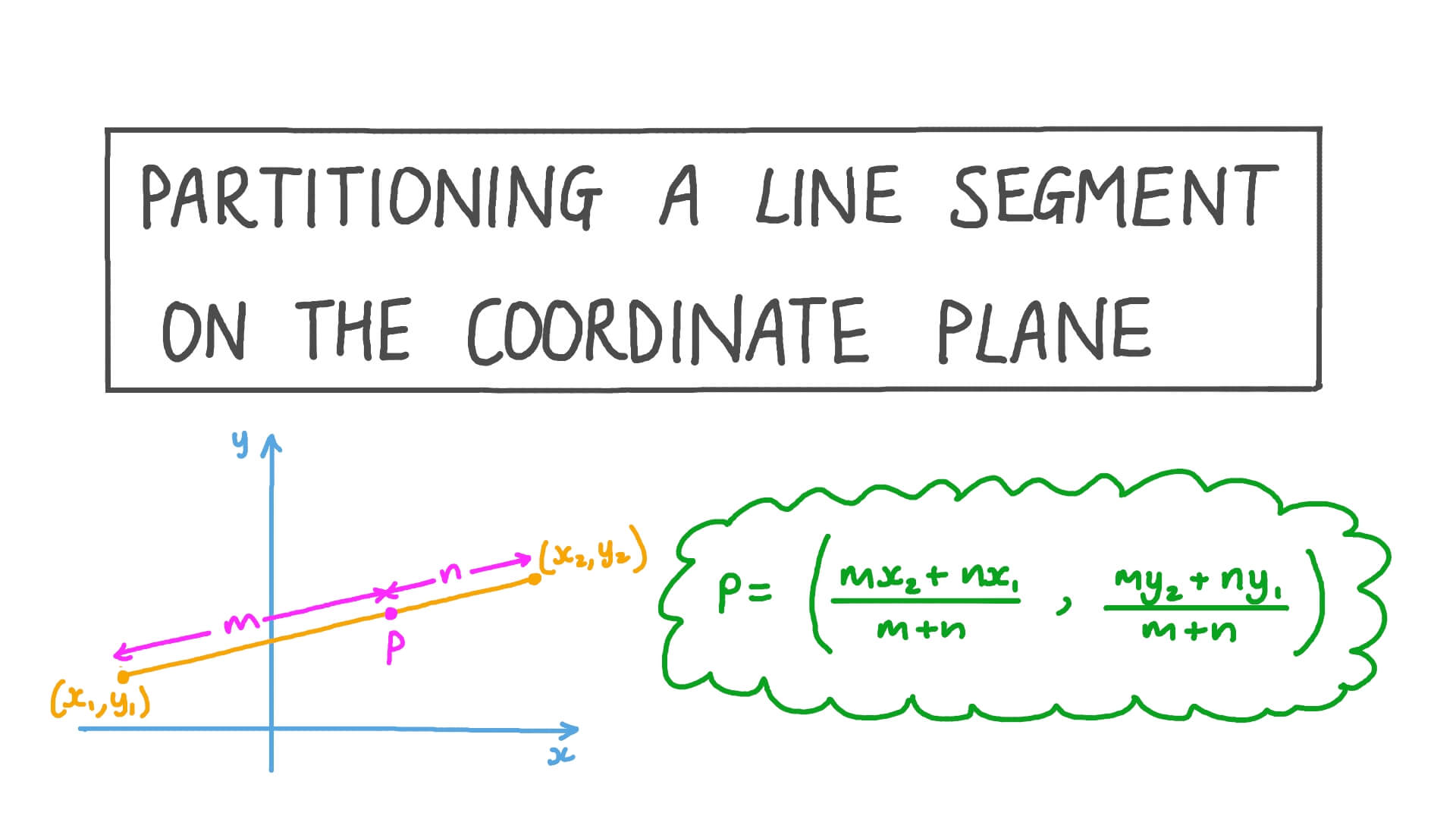
In this lesson, we will learn how to find the coordinates of a point that divides a line segment on the coordinate plane with a ratio using the section formula.
Lesson Plan
Lesson Presentation
Lesson Video
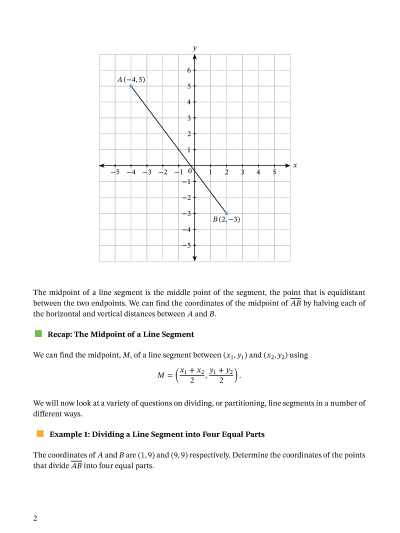
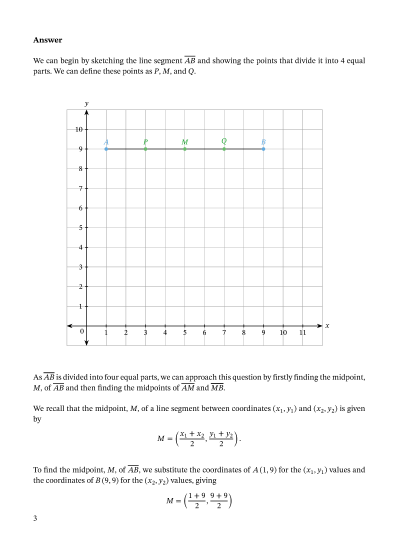
Lesson Explainer
Lesson Playlist
-
 +6
03:35
+6
03:35